Стивен Вольфрам: кажется, мы близки к пониманию фундаментальной теории физики, и она прекрасна

В продолжение моего поста про вычислимую Вселенную я хочу представить вам свой перевод статьи Стивена Вольфрама, созданной в рамках его проекта The Wolfram Physics Project.

Неожиданное открытие

За прошедшие несколько веков произошел настоящий прорыв в наших знаниях о принципах работы окружающего нас мира. Но несмотря на это, у нас все еще нет фундаментальной теории физики, и мы все так же не имеем ответа на вопрос о том, как именно работает наша Вселенная. Я занимаюсь этой темой уже порядка 50-и лет, но только в последние несколько месяцев все кусочки пазла наконец-то начали складываться вместе. И получающаяся картина оказалась гораздо прекрасней, чем все, что я только мог себе представить.

В те времена, когда я зарабатывал себе на жизнь теоретической физикой, я не особо задумывался над поиском так называемой «теории всего». Я был больше озабочен тем, чтобы извлечь что-нибудь новое из тех теорий, которые у нас уже есть. И я думал, что даже если когда-нибудь и появится единая фундаментальная теория физики, то она неизбежно окажется очень сложной и запутанной.

Но когда в начале 80-х я начал изучать теорию клеточных автоматов, я осознал, что работающие даже по очень простым правилам системы могут иметь поразительно сложное поведение. И это натолкнуло меня на мысль: может быть Вселенная устроена схожим образом? Может быть под всей кажущейся сложностью и многогранностью нашей Вселенной скрываются очень простые правила?

В начале 90-х годов у меня сформировалось некоторое понимание того, как эти правила могли бы выглядеть, и ближе к концу того десятилетия я начал понимать, как из этих простейших правил мы можем вывести наши знания о пространстве, времени, гравитации и всех других физических явлениях. Этим идеям «вычисления» законов физики я посвятил около 100 страниц в своей книге A New Kind of Science.

Мне всегда хотелось начать большой исследовательский проект, чтобы продвинуться в этом направлении дальше. Я пытался начать такой проект в 2004 году, но сильно увяз в работе над Wolfram Alpha и Wolfram Language. Время от времени я встречался со своими друзьями-физиками и мы обсуждали мои идеи. Это были интересные разговоры, но мне казалось, что поиск фундаментальной теории физики — это слишком сложное занятие, доступное только реально увлеченным фанатикам.

Было что-то, что сильно беспокоило меня в моих идеях. Правила, определяемые моей теорией, казались мне слишком негибкими и надуманными. Как создатель языка для математических вычислений, я постоянно думал об абстрактных системах правил. И очень часто у меня было ощущение, что что-то подобное может быть и в физике. Но мои рассуждения никогда никуда меня не приводили. Пока внезапно осенью 2018 года у меня не появилась интересная идея.

В некотором смысле эта идея была простой и очевидной, хотя и очень абстрактной. Но кроме того, она была очень элегантной и минималистичной. Мне показалось, что я очень близок к пониманию того, как работает наша Вселенная. К сожалению, я был жутко занят развитием Wolfram Alpha, и не смог выделить времени на еще один проект. Все изменилось, когда на нашей ежегодной летней школе в 2019 году я встретил двух молодых физиков — Джонатана Горарда и Макса Пискунова, которые вдохновили меня наконец-то сесть за проработку своих идей. Физика всегда была моей страстью, и вот после своего 60-летнего юбилея в августе 2019 года я наконец-то решился сделать это.

Итак, вместе с двумя вдохновившими меня молодыми физиками в октябре 2019 года мы начали наш проект. И не успев начать наши исследования, мы сразу же стали наталкиваться на очень интересные находки. Мы воспроизвели все, что я разрабатывал в 90-х годах, но гораздо более элегантным способом. Из маленьких бесструктурных правил мы вывели пространство, время, относительность, гравитацию и намеки на квантовую механику.

Мы провели миллионы экспериментов, проверяя свои догадки. Постепенно все начало проясняться, мы начали примерно понимать как работает квантовая механика. Мы поняли, что такое энергия. Мы вывели формулировку квантовой теории через интегралы по траекториям, созданную моим покойным другом и учителем Ричардом Фейнманом. Мы увидели некоторые глубокие структурные связи между относительностью и квантовой механикой. Все встало на свои места. Мы начали понимать не только как работают законы физики, но и почему.

Я и мечтать не мог о том, что наш прогресс будет настолько стремительным. Я ожидал, что наши исследования будут идти гораздо медленнее, что если повезет, мы будем потихоньку продвигаться в понимании законов физики и того, что происходило с нашей Вселенной в первые секунды ее существования, и что мы потратим долгие годы на эти изыскания. В конце, если у нас будет полная фундаментальная теория физики, мы сможем найти конкретную единую формулу для нашей Вселенной. И даже сейчас я не знаю, как долго это займет: год, десятилетие или даже целый век. Несколько месяцев назад я не был даже уверен, что мы на верном пути. Но сегодня все изменилось. Слишком многое встало на места. Мы еще не знаем точных деталей и того как именно настроены шестеренки нашего мира, но я полностью уверен, что имеющаяся у нас модель однажды расскажет нам о том, как устроена Вселенная.

Самый верный признак качества научной модели — простые законы объясняют сложные эффекты. И наша теория как никакая другая соответствует этому эмпирическому правилу. Из простейших формул мы получаем целые разделы современной физики. И что наиболее удивительно — нам до сих пор не пришлось вводить для этого никаких дополнительных параметров. Мы просто ищем объяснения физических явлений в самих свойствах нашей модели, не добавляя ничего сверх того.

В основе нашей модели лежат настолько простые правила, насколько это только возможно. Забавно, что эти правила могут быть записаны в одну строчку на Wolfram Language. В сыром виде, они не очень похожи на все те математические структуры, что мы знаем. Но как только мы смотрим на результаты многоитерационного рекурсивного применения этих правил, то становится ясно насколько элегантно они связаны с современной математикой. То же самое и с физикой. Базовая структура наших моделей выглядит абсолютно чуждой всему, что было сделано в физике за последние несколько столетий. Но то, что мы получили изучая наши модели, было изумительно: мы обнаружили, что многие теории, созданные физиками в последние десятилетия, отлично ложатся на нашу модель.

Я боялся, что мне придется выкинуть все существующие достижения науки. Но оказалось, что несмотря на то, что наша модель, подход и методы очень сильно отличаются от всех существующих, в основе нашей теории лежит все то, над чем физики работают последние десятки лет.

После мы начнем физические эксперименты. Если бы вы спросили меня пару месяцев назад, когда мы получим какие-либо проверяемые выводы из наших моделей, я бы ответил, что нескоро и точно до того, как мы найдем финальную формулу. Но сейчас мне кажется, что я был неправ. И фактически мы уже получили некоторые догадки о неизведанных причудливых явлениях, существование которых можно экспериментально подтвердить.

Что же дальше? Я буду рад сказать, что я думаю, что мы нашли дорогу к фундаментальной теории физики. Мы построили парадигму, фреймворк и вычислительные инструменты для нее. Но теперь мы должны закончить работу. Мы должны проделать тяжелую работу по физическим, математическим и алгоритмическим расчетам и узнать, можем ли мы наконец-то ответить на мучающий нас тысячелетиями вопрос о том, как работает наша Вселенная.

Я хочу разделить с вами этот волнующий момент. Я с нетерпением жду того, чтобы многие люди приняли участие в нашем проекте. Этот проект ведь не только мой и моей маленькой команды. Это проект важный для всего мира. И когда мы закончим его, он станет нашим величайшим достижением. Поэтому я хочу, чтобы как можно больше людей поучавствовали в нем. Да, многое, что нужно сделать, требует нетривиальных познаний в физике и математике, но я хочу распространить информацию о проекте как можно шире, чтобы каждый мог внести свой вклад и вдохновиться тем, что станет величайшим в истории интеллектуальным приключением.

Мы официально запускаем наш Wolfram Physics Project. Начиная с сегодняшнего дня мы будем транслировать все, что мы делаем и делиться нашими открытиями со всем миром в реальном времени. Я публикую все наши материалы и весь наш софт для расчетов. Мы будем постоянно выкладывать сводки о нашем прогрессе и различные образовательные материалы.

Также мы выкладываем в открытый доступ Реестр Замечательных Вселенных. Он заполнен примерно тысячью правил. Я не думаю, что даже хотя бы одно из них относится к нашей Вселенной, хотя я и не могу быть полностью уверенным в этом. Но однажды, и я надеюсь это однажды наступит уже очень скоро, в нашем реестре появится правило, полностью описывающее нашу Вселенную.

Общие принципы

Так как же работает наша модель? Я написал 448-страничное техническое изложение наших идей (да, я изрядно поработал в течение предыдущих нескольких месяцев). Другой член нашей команды Джонатан Горард написал две 60-страничные технических статьи. На странице нашего проекта доступно еще несколько материалов по данной теме. Но в этой статье я собираюсь дать краткое изложение общих положений нашей теории.

Все начинается с самого простого множества абстрактных отношений между абстрактными элементами, которое также может быть представлено в виде графа.

Предположим, у нас есть множество отношений:
{{1, 2}, {2, 3}, {3, 4}, {2, 4}}
которое в виде графа выглядит так:


Все, что мы определяем здесь — это отношения между элементами (например {1, 2}). Порядок, в котором мы объявляем эти отношения, не имеет значения, а вот порядок элементов внутри каждого отношения важен. И при зарисовке графа имеет значение только то, что с чем соединено. Фактическое расположение элементов на рисунке выбрано только из соображений красоты и ничего другого. Также не имеет значения, как называются элементы. Я пронумеровал их на рисунках, но можно было бы этого и не делать.

Так что же мы будем делать с этими графами? Мы будем применять к ним очень простое правило много много раз. Вот пример подобного правила:
{{x, y}, {x, z}} → {{x, z}, {x, w}, {y, w}, {z, w}}
Это правило гласит, что мы должны взять два отношения из множества и проверить их на соответствие образцу {{x,y},{x,z}}. Если есть совпадение, то мы заменяем эти два отношения четырьмя отношениями {{x, z}, {x, w}, {y, w}, {z, w}} (где w — это новый элемент множества).

Мы можем представить эту трансформацию как операцию над графами:

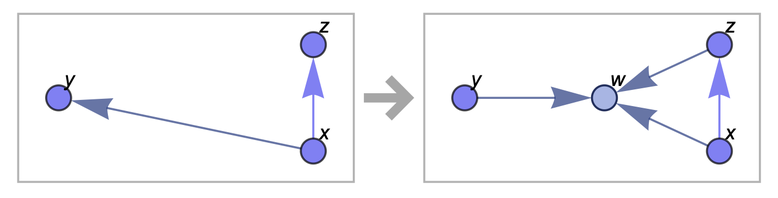
Теперь давайте применим это правило к нашему множеству:
{{1, 2}, {2, 3}, {3, 4}, {2, 4}}
Отношения {2,3} и {2,4} соответствуют нашему образцу, так что мы заменяем их на четыре новых отношения и получаем:
{{1, 2}, {3, 4}, {2, 4}, {2, 5}, {3, 5}, {4, 5}}
Мы можем представить результат в виде графа (я нарисовал его перевернутым по отношению к изначальному):

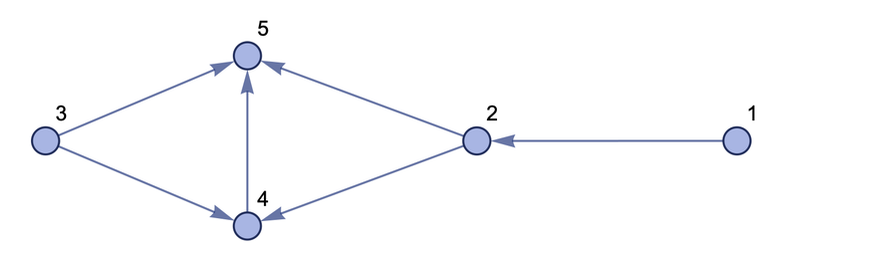
Что будет, если мы продолжим применять это правило к нашему множеству рекурсивно? Результат будет выглядеть так:

Давайте сделаем это еще пару раз и получим более общую картину:


Что произошло? У нас было очень простое правило. Но рекурсивное применение этого правила породило структуру, выглядящую очень сложным образом. Здравый смысл подсказывает нам, что так не бывает. Но в действительности такое спонтанное зарождение сложности встречается повсеместо при применении простейших правил к простейшим структурам. Вся моя книга A New Kind of Science посвящена этому феномену и тому, почему изучение этого феномена критически важно для современной науки.

Именно из таких простых структур и правил мы выведем принципы работы нашей Вселенной и всего, что в ней есть. Давайте еще раз посмотрим на то, что мы сделали. Мы взяли простое множество абстрактных отношений и стали рекурсивно применять к нему простое правило преобразования. Но то, что мы получили, простым назвать никак нельзя. И самое главное, у получившегося объекта становится заметна некая форма. Мы не вкладывали никакого смысла в эту форму. Мы просто взяли простейшее правило, и используя это правило мы построили граф. При визуализации этого графа мы видим, что он принимает определенную форму.

Если мы исключим всю материю во Вселенной, то окажется, что наша Вселенная это просто громадный кусок пространства. Но что такое пространство? У нас есть математические абстракции пространства уже более двух тысяч лет. Но что это пространство? Состоит ли оно из чего-то, и если состоит, то из чего именно?

Я думаю, что пространство похоже на картинки сверху — это целый сгусток связанных друг с другом абстрактных точек. Только на картинке сверху всего 6704 точек, тогда как в реальной Вселенной их около 10^400 или даже больше.

Все возможные правила

Мы пока не знаем точное правило, отражающее нашу Вселенную — и это точно не то правило, которое мы только что рассматривали. Так давайте же обсудим какие возможные правила бывают, и что из них получается.

Характерной чертой правила, которое мы рассматривали выше, было то, что оно работает с множествами бинарных отношений, содержащих пары элементов (например {1, 2}). Но та же самая система может работать с отношениями, содержащими большее количество элементов. Вот например, множество из двух троичных отношений:
{{1, 2, 3}, {3, 4, 5}}

Мы не можем представить это множество в виде обычного графа, но мы можем использовать гиперграф — конструкцию, в которой мы обобщаем ребра графа, которые соединяют пары точек, в гипер-ребра, соединяющие любое количество точек:

Заметьте, что мы имеем дело с направленными гиперграфами, где порядок, в котором находятся точки в гипер-ребре имеют значение. На этой картинке «мембраны» просто означают то, какие точки соединены в одно гипер-ребро.

Мы точно так же можем задать правила для гиперграфа:
{{x, y, z}} → {{w, w, y}, {w, x, z}}


И вот что будет, если мы применим это правило к простейшему возможному троичному множеству {{0,0,0}}: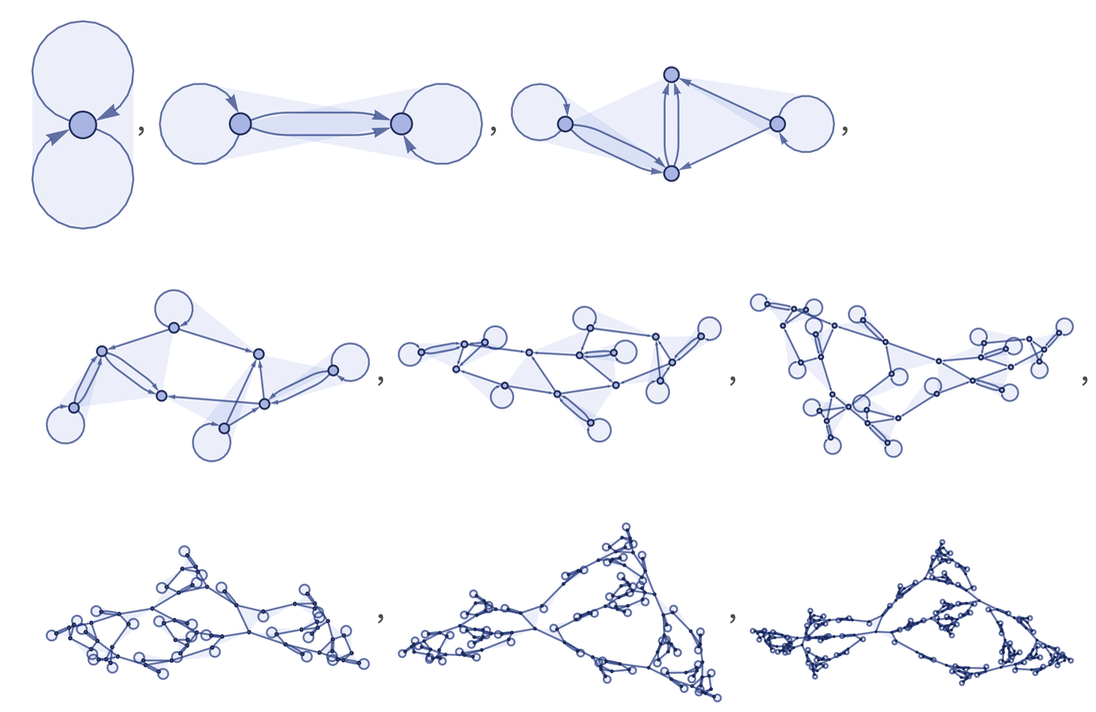


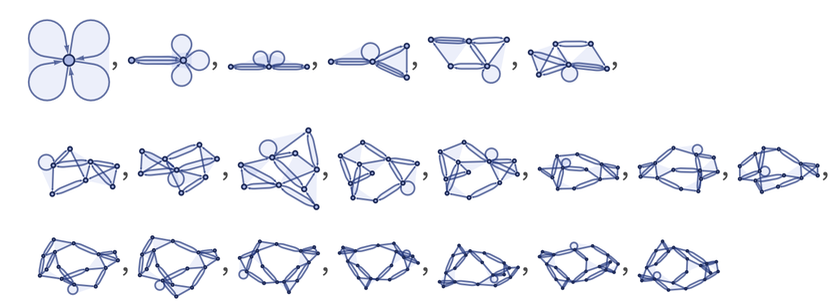
Отлично! В таком случае, что будет, если мы начнем запускать разные случайные простые правила? Вот некоторые результаты таких запусков:

Вам не кажется, что все эти структуры выглядят очень «по-живому»? И да некоторые эти модели определенно могут иметь отношение не только к фундаментальной физике, но и например к конструкции биологических клеток. По факту, мы видим здесь различные общие формы поведения. Некоторые из них простые, некоторые не очень.

Вот примеры типов структур, которые мы видим:


Главный вопрос состоит в том, что: если мы будем прогонять эти правила достаточно долго, выдадут ли они нам результат, воспроизводящий нашу физическую Вселенную? Или формулируя по-другому, можем ли мы найти в этой вычислимой по простым правилам математической структуре нашу физическую Вселенную?

И даже если наша физическая Вселенная там присутствует, как мы можем в этом убедиться? Все что мы видим на картинках выше — результат нескольких тысяч итераций. В нашей настоящей Вселенной было произведено около 10^500 итераций, а может быть даже больше. Преодолеть эту разницу непросто. И мы должны идти к разрешению этой проблемы с обеих сторон. С одной стороны, мы должны использовать все наши знания о физике нашей Вселенной, которые мы получили за предыдущие несколько сотен лет. С другой стороны, мы должны изучать эти самые простейшие правила преобразования графов и понимать, что именно они делают.

И даже здесь есть потенциально фундаментальная проблема: феномен вычислительной несократимости. Одно из величайших достижений математики произошло около трех столетий назад: были изобретены уравнения и формулы, которые говорили как система ведет себя без описания каждого шага, который эта система совершает. Но еще много лет назад я понял, что в вычислимой Вселенной очень часто сделать это оказывается невозможно. Даже если вы знаете точное правило, по которому работает система, вы не можете понять, как эта система работает без выполнения каждого шага вычисления.

Вы можете подумать, что если мы знаем правило, которому следует система — тогда, используя всю вычислительную мощь наших компьютеров и мозгов, мы всегда можем «запрыгнуть вперед» и понять, как система будет вести себя. Но в действительности этому мешает эмпирический закон, который я называю Принципом Вычислительного Равенства — почти в любом случае, когда поведение системы не очевидно простое, то не существует алгоритма расчета состояния системы после определенного количества итераций с вычислительной сложностью меньшей, чем вычислительная сложность осуществления всех этих итераций. Так что мы не сможем «обогнать» вычисление, и чтобы понять, как система работает, нам придется выполнить несократимое количество шагов.

Для наших моделей это может оказаться потенциально большой проблемой. Потому что мы не можем даже приблизиться по количеству выполняемых итераций к тому числу итераций, которое произвела наша Вселенная с начала своего существования. Также не совсем понятно, сможем ли мы извлечь достаточно информации из прогонки наших моделей на доступных нам вычислительных мощностях и понять, как эта информация соотносится с известными нам законами физики.

Самым большим сюрпризом для меня стало то, что, кажется, нам везет. Мы знаем, что даже когда в нашей системе есть вычислительная несократимость, в ней также есть бесконечное число зон вычислительной сократимости. И большинство этих зон соответствуют нашим знаниям о физике.

Что такое пространство?

Давайте взглянем на одно простое правило из нашей громадной коллекции:
{{x, y, y}, {z, x, u}} → {{y, v, y}, {y, z, v}, {u, v, v}}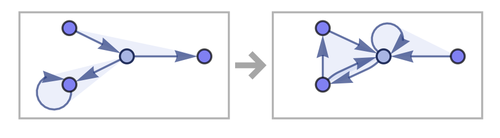


Вот что оно порождает:

А через еще несколько итераций получается вот это:

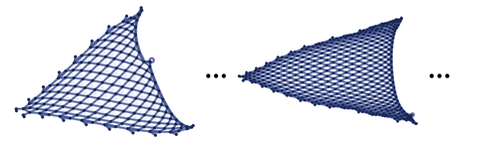
Получившаяся структура сильно напоминает очень простой «кусочек пространства». Если мы продолжим рекурсивно применять наше правило дальше, то эта сетка будет становиться все тоньше и тоньше, пока в конце концов не станет неотличима от сплошной плоскости.

Вот другое правило:
{{x, x, y}, {z, u, x}} → {{u, u, z}, {v, u, v}, {v, y, x}}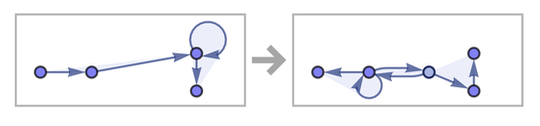



Эта структура уже напоминает трехмерную. А вот еще одно правило:
{{x, y, z}, {u, y, v}} → {{w, z, x}, {z, w, u}, {x, y, w}}



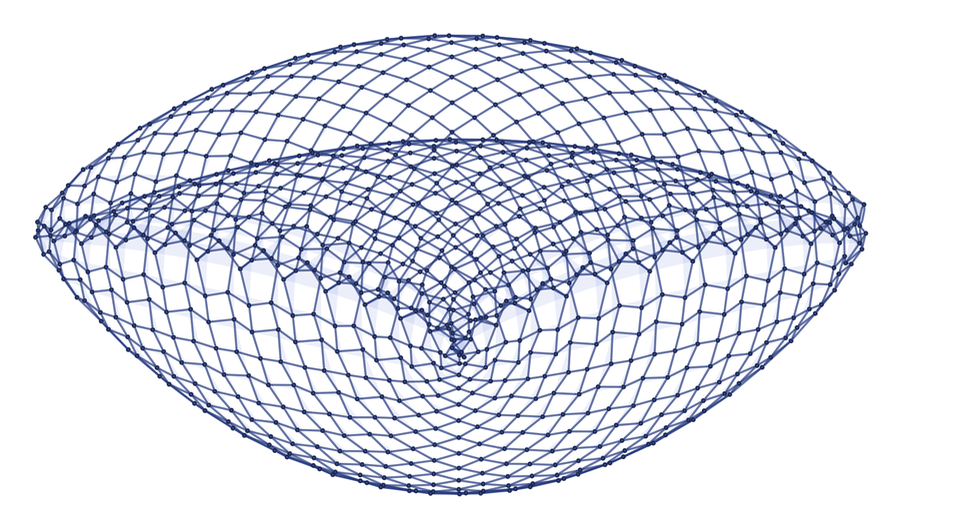
Это не кажется вам странным? У нас есть правило, которое определяет как переписывать куски абстрактного гиперграфа без какого либо упоминания геометрии или трехмерного пространства. И после определенного количества итераций это правило порождает гиперграф, выглядящий как трехмерная поверхность.

И несмотря на то, что тут в действительности есть только связи между точками, мы можем «догадаться» на какой фигуре может быть такая поверхность и отрендерить результат в трех измерениях:

Если мы продолжим, то постепенно сетка будет становиться все тоньше и тоньше, пока не превратится в непрерывную 3D поверхность, которую вы могли бы изучать на курсе матанализа. Конечно, в некотором роде это не «настоящая» поверхность — это просто гиперграф, представляющий кучу абстрактных отношений, но каким-то образом паттерн этих отношений делает структуру все более и более похожей на поверхность.

И я думаю, что именно так устроено все пространство в нашей Вселенной. В общем-то это куча дискретных, абстрактных отношений между абстрактными точками. Но при взгляде с определенного масштаба мы видим, что паттерн этих отношений делает эту структуру похожей на привычное нам непрерывное пространство. Это похоже на наше представление о воде: по сути вода — это куча дискретных молекул, но когда мы смотрим на нее с большого масштаба, она кажется нам непрерывной жидкостью.

Люди размышляли о том, что пространство может быть дискретным с античности, но в современную физику вписать эту концепцию ни у кого не получалось. Да и гораздо удобнее рассматривать пространство как континуум, чтобы была возможность использовать всю мощь созданного нами математического аппарата. Но сейчас мне кажется, что идея о том, что пространство дискретно, точно войдет в фундаментальную теорию физики.

Размерность пространства

Мы ощущаем пространство как трехмерное. Как наши правила могут воспроизвести эту трехмерность? Два правила, которые мы только что рассмотрели, породили двумерные поверхности: в первом случае плоскую, во втрором имеющую некую форму. Конечно, это не очень честные примеры двумерного пространства — это просто сетки, которые распознаются нами как поверхности. С нашей Вселенной дела обстоят иначе, она устроена гораздо сложнее.

Давайте тогда рассмотрим такой случай:


Если мы будем продолжать применять создавшее эту картину правило еще много много раз, получим ли мы что-то вроде пространства, и если да, то сколько измерений будет у такого пространства? Чтобы получить ответ на этот вопрос, мы должны определить не допускающий возражений способ определения количества измерений. Но помните, нарисованные мною картинки — это просто визуализация структуры, являющейся сгустком дискретных отношений или гиперграфом без какой-либо информации о координатах, геометрии или даже топологии. Отдельно подчеркну, что этот граф можно отрисовать еще кучей разных способов:


Для того, чтобы определить количество измерений, нам нужно вспомнить, что площадь круга вычисляется как πr^2, а объем сферы как 4/3 π r^3. В общем случае, «объем» d-мерного аналога сферы равен константе умноженной на r^d. Давайте вернемся к нашему гиперграфу и выберем случайную начальную точку. Затем мы обведем r гиперребер всеми возможными способами. Таким образом у нас получается аналог «сферического шара» на гиперграфе. Вот примеры гиперграфов, соответствующих двухмерным и трехмерным пространственным решеткам:



И если вы посчитаете количество точек, достигнутых обводкой «графовым радиусом r», вы обнаружите, что их количество в данных двух случаях растет как r^2 и r^3 соответственно. Таким образом мы получаем способ определения измерения нашего гиперграфа. Просто начинаем в определенной точке и смотрим, как много точек мы можем достигнуть, обрисовывая r ребер:


Теперь чтобы определить точное значение кол-ва измерений, нам нужно соотнести получившийся результат с r^d. Нужно учитывать, что не стоит брать слишком маленький r, при котором структура графа может сильно повлиять на результат, или слишком большой r, при котором мы можем упереться в край. Также мы должны учитывать как это «пространство» эволюционирует с каждой итерацией. Учитывая эти ограничения, мы можем провести серию расчетов для точного определения измерений. Проведя расчет для рассматриваемого нами выше примера, мы получим число измерений примерно равное 2.7:

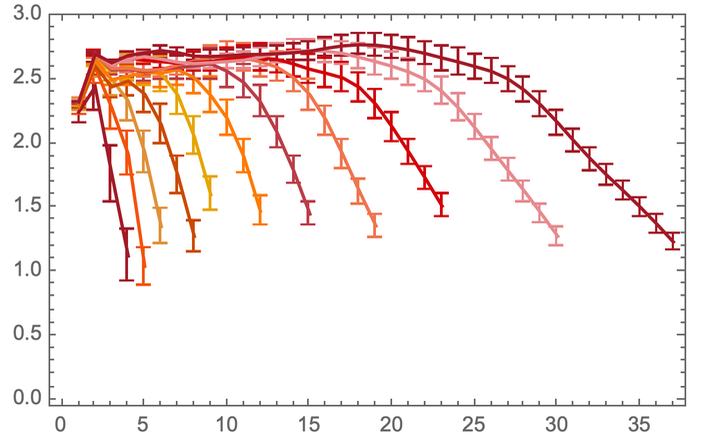
Если мы проделаем то же самое для вот этого графа:

Количество измерений стремится к 2-м, как и должно:


Но что означает нецелое значение числа измерений? Давайте рассмотрим фракталы, которые мы легко можем создать с помощью такого правила:
{{x, y, z}} → {{x, u, w}, {y, v, u}, {z, w, v}}


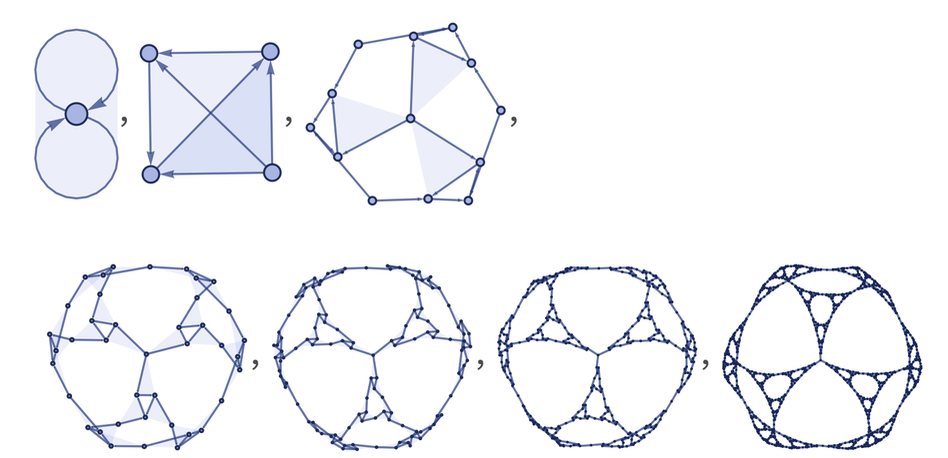
Если мы замерим количество измерений для этого фрактала, то получим log2(3)=1.58 — обыкновенное нецелое измерение для треугольника Серпинского:

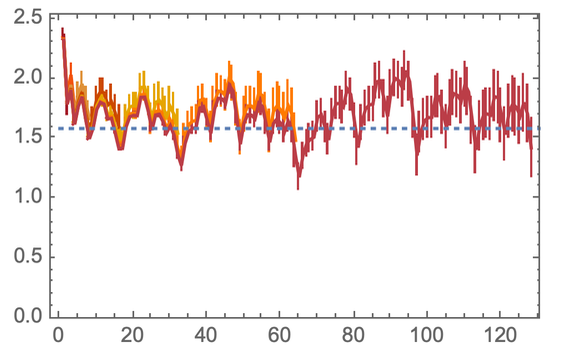
Из рассматриваемого нами выше правила не получается такой же ровной структуры как эта. Фактически, даже если правило само по себе полностью детерминировано, порождаемая им структура может быть совершенно случайной формы. Но наши измерения предполагают, что при достаточном количестве итераций это правило производит на свет что-то похожее на 2.7-мерное пространство.

Разумеется, 2.7 это не 3, и по-видимому это конкретное правило не является правилом нашей Вселенной (хотя не известно какое количество измерений получится у этого пространства, если мы прогоним это правило хотя бы 10^100 итераций). Но определение количества измерений показывает пример того, как мы можем начать делать физические предположения о поведении наших правил.

Кстати, мы говорили о «появлении пространства» в наших моделях, но в действительности таким образом появляется не только пространство, но и все остальное, что есть во вселенной. В современной физике пространство описано многообразно и служит, так сказать, фоном для всего остального: материи, частиц, планет и так далее.

Но в наших моделях в известном смысле нет ничего кроме пространства: то есть все во Вселенной должно «состоять» из пространства. Или если перефразировать, то тот же самый гиперграф, который порождает пространство, порождает также и все остальное, что существует в этом пространстве. Это значит, что, например, частица вроде электрона или фотона должна соответствовать какому-то простому свойству гиперграфа. Как вот в этом игрушечном примере:


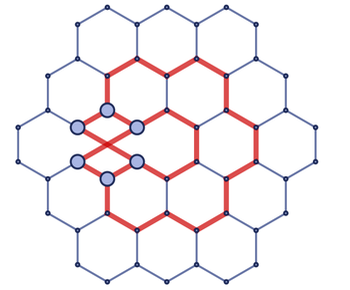
По моим оценкам, в 10^200 раз больше сил гиперграф тратит на «поддержку» структуры пространства, чем на «поддержку» всей существующей во Вселенной материи.

Искривление пространства и уравнения Эйнштейна

Вот простые примеры некоторых структур, которые порождаются нашими правилами:


Все они похожи на поверхности, но они очевидно разные. И единственный способ как-то характеризовать их — по их локальной кривизне. Получается, что в наших моделях искривление — это концепт, тесно связанный с количеством измерений. Этот факт критически важен для понимания, например, того, почему возникает гравитация.

Но для начала, давайте поговорим о том, как можно измерить кривизну гиперграфа. Обычно площадь круга равна πr^2 Но давайте представим, что мы нарисовали круг на поверхности сферы и теперь мы пытаемся найти его площадь: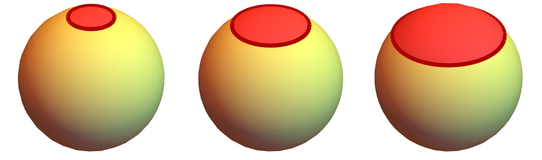

Теперь площадь не равна πr^2. Вместо этого она высчитывается по формуле πr^2 \* (1 - r^2/12a^2 + r^4/360a^4 - ...), в которой a — это радиус сферы. Другими словами, чем больше становится радиус нарисованного круга, тем больше на его площадь влияет тот факт, что он нарисован на поверхности сферы. Представьте круг, нарисованный на глобусе вокруг Северного Полюса — самый большой из таких возможных кругов пройдет по экватору.

Если мы обобщим эту формулу для d измерений, то получится такая формула роста «объема»: r^d(1-Rr^2/6(d+2)+...), где R — это математический объект, называющийся скалярной кривизной Риччи.

Это означает, что если мы рассмотрим скорость роста сферических шаров в нашем гиперграфе, мы можем ожидать двух соответствий: во-первых эта скорость соответствует r^d, во-вторых «коррекция» этой скорости благодаря искривлению равна r^2.

Вот пример. Вместо оценки количества измерений (в данном случае равному 2), мы описываем плавно опускающуюся переменную, соответствующую положительной (как у сферы) кривизне поверхности:


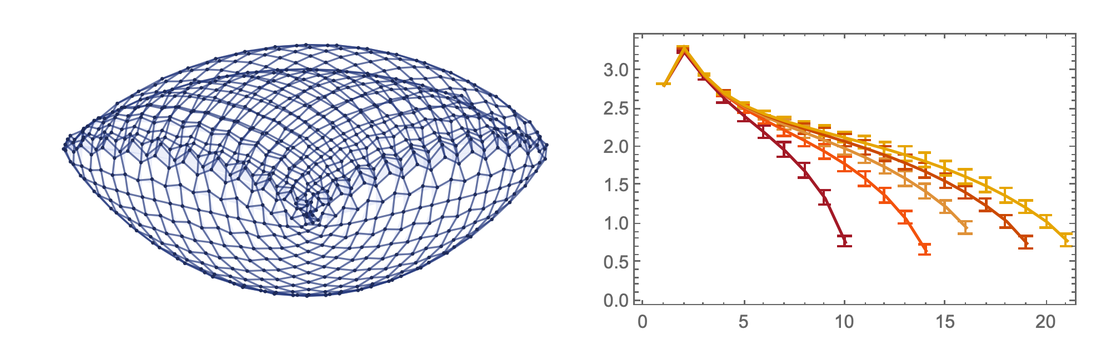
Но в чем значение кривизны? Во-первых она имеет применение в геодезии. Геодезическая линия — это наикратчайшее расстояние между двумя точками. В плоском пространстве это прямая, но в искривленном пространстве геодезические линии тоже искривлены:


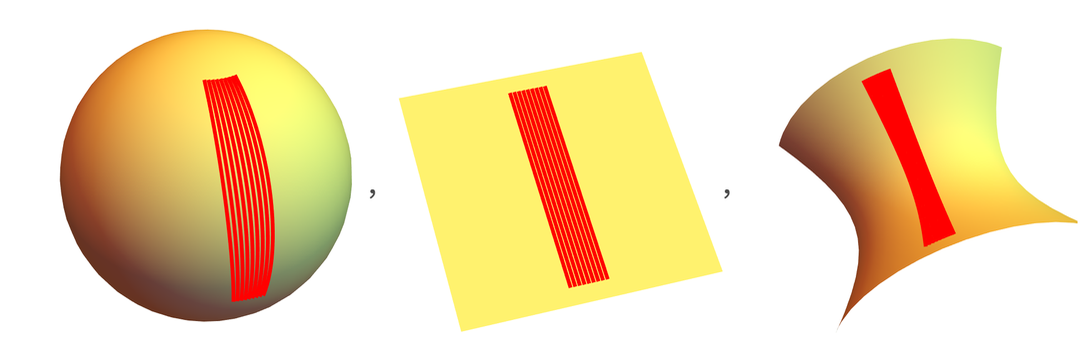
В случае положительной кривизны пучки геодезических линий сходятся, в случае отрицательной кривизны они расходятся. Даже учитывая то, что геодезические линии были изначально определены для непрерывного пространства, они могут присутствовать и в графах. Для графов определение геодезической линии точно такое же — это наикратчайший путь между двумя точками на графе.

Вот геодезические линии на поверхности с положительным искривлением, порожденной одним из наших правил:

А вот геодезические линии в более сложной структуре:


Почему эти геодезические линии так важны? Причина в том, что в общей теории относительности Эйнштейна свет распространяется по траектории, соответствующей геодезическим линиям. И гравитация в этой теории соотносится с кривизной пространства. То есть когда что-нибудь отклоняется от траектории вокруг Солнца, то это происходит потому что пространство вокруг Солнца искривлено и геодезическая линия этого предмета так же искривлена.

Описание искривления пространства в общей теории относительности основывается на скалярной кривизне Риччи R, о которой мы говорили выше. Но если мы хотим понять, как наши модели воспроизводят уравнения Эйнштейна для гравитации, мы должны выяснить, что кривизна Риччи, получающаяся из наших гиперграфов соответствует кривизне, предполагаемой теорией относительности.

Здесь нам придется прибегнуть к небольшим математическим изысканиям (например, мы будем рассматривать кривизну пространства-времени, а не просто пространства). Вкратце, в различных пределах и при определенных допущениях наши модели действительно воспроизводят уравнения Эйнштейна. Сначала мы воспроизведем уравнения для вакуума без материи. Затем, когда мы будем обсуждать природу материи, мы увидим, что мы действительно получим полные уравнения Эйнштейна.

Это очень непростая задача — воспроизвести уравнения Эйнштейна. Обычно в физике все начинается с этих уравнений, но у нас они появляются из свойств самой модели.

Я думаю, стоит немного рассказать про то, как работает этот вывод. Это что-то похожее на вывод уравнений потока жидкости из уравнений динамики множества дискретных молекул, из которых эта жидкость состоит. В нашем случае, мы вычисляем скорее структуру пространства нежели скорость жидкости. Хотя для этого нам нужно сделать ряд очень похожих математических приближений и допущений. Примем, к примеру, что случайность, присутствующая в системе, годна для того, чтобы к ней была хорошо применима статистика. Также есть еще куча хитрых математических ограничений. Например, расстояния должны быть огромны по сравнению с длиной ребра гиперграфа, но достаточно маленькими по сравнению с общим размером графа, и так далее.

Достаточно часто физики «забивают» на математические тонкости. Например, около века такое продолжалось в случае с получением уравнений потока жидкости из молекулярной динамики. И нас можно обвинить в том же самом. По-другому говоря, нужно сделать еще довольно много математической работы, чтобы наш вывод был действительно строгим и тщательным, и мы в точности понимали бы его границы применимости.

Кстати, говоря о математике, даже имеющаяся у нас структура интересна. Математический анализ был разработан для работы в простом непрерывном пространстве (многообразия, которые приближены к Евклидовому пространству). Но то, что есть у нас — иное: в пределах бесконечно большого гиперграфа мы имеем нечто, очень похожее на непрерывное пространство, но обыкновенный матанализ неприменим (как минимум потому что у нашего гиперграфа может быть нецелый показатель количества измерений). Так что нам нужно изобрести некое обобщение математического анализа, которое, к примеру, может иметь дело с искривлением нецело-мерного пространства. Наверное, самая близкая к этой задаче область современной математики — геометрическая теория групп.

Кстати, нужно отметить, что существует много тонкостей в нахождении компромисса между изменением размерности пространства и наличием кривизны в нем. И несмотря на то, что нам кажется, что мы живем в трехмерной Вселенной, вполне возможны локальные отклонения и скорее всего существовали громадные отклонения в ранней Вселенной.

Время

В наших моделях пространство определено структурой гиперграфа, отображающего множество абстрактных отношений. Но что же такое время?

В прошлом столетии в фундаментальной физике была принята точка зрения, что время «подобно пространству», и что нам следует соединять время и пространство в одну сущность и говорить о пространственно-временном континууме. И теория относительности указывает в данном направлении. Но если и был один «поворот не туда» в истории физики в прошлом веке, я думаю, это было предположение, что время и пространство имеют родственную природу. И несмотря на то, что в наших моделях это не так, как мы увидим, относительность прекрасно из них выводится.

Так что же тогда такое время? По сути, оно в точности такое, как мы его чувствуем: неумолимый процесс протекания событий и их влияния на последствия. Но в наших моделях оно является нечтом гораздо более точным: это последовательное применение правил, которые постоянно изменяют абстрактную структуру, определяющую содержимое вселенной.

Модель времени в наших моделях в некотором смысле очень вычислительная. По прошествии времени мы фактически видим результаты все большего числа шагов в вычислении. И действительно, феномен вычислительной несократимости подразумевает, что этим процессом «достигается» нечто определенное и несокращаемое. (И, например, несократимость — это то, что я считаю ответственным за «шифрование» начальных условий и связанным с законом увеличения энтропии и термодинамической стрелой времени.) Само собой разумеется, что современной информатики не существовало сто лет назад, когда было введено «пространство-время», а ведь история физики могла бы быть совершенно другой.

В наших моделях время — это просто последовательное применение правил. Но в том, как оно работает, есть тонкость, которая на первый взгляд может показаться мелочью, но на самом деле она оказывается ключом как к теории относительности, так и к квантовой механике.

В начале этой статьи я говорил о правиле:
{{x, y}, {x, z}} → {{x, z}, {x, w}, {y, w}, {z, w}}

и показал первые несколько шагов применения этого правила:


Но как именно применялось правило? Что «внутри» этих шагов? Правило определяет, как взять два ребра в гиперграфе (который в данном случае фактически является просто графом) и преобразовать их в четыре новых ребра, создав тем самым новый элемент. Таким образом, каждый «шаг», который мы показали ранее, на самом деле состоит из нескольких отдельных «событий обновления» (здесь новые добавленные соединения выделены, а те, которые собираются удалить, отмечены пунктиром):


Это не единственная последовательность событий обновления, соответствующая правилу. Правило просто говорит, что нужно найти два соседних соединения, и если есть несколько возможных вариантов, ничего не говорится о том, какое из них «правильное». И основная идея в нашей модели — просто реализовать их все.

Мы можем представить это в виде графа, показывающего все возможные пути:


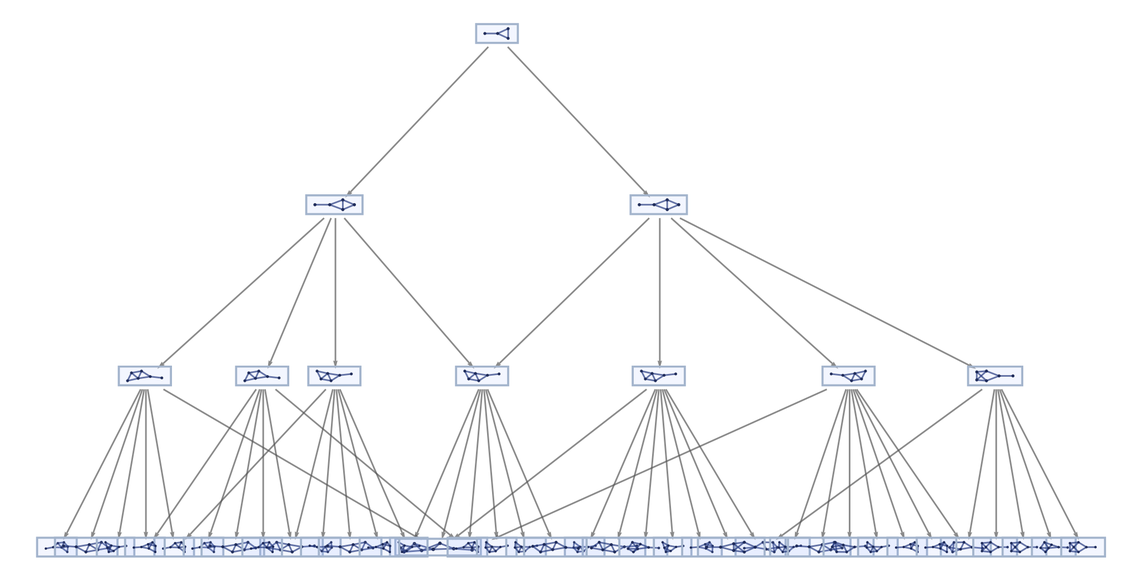
Для самого первого обновления есть две возможности. Затем для каждого из этих результатов есть четыре дополнительных возможности. Но при следующем обновлении происходит кое-что интересно: две ветки сливаются. Другими словами, даже если мы выполнили разные последовательности обновлений, результат — один и тот же.

Все быстро усложняется. Вот граф после еще одного обновления:


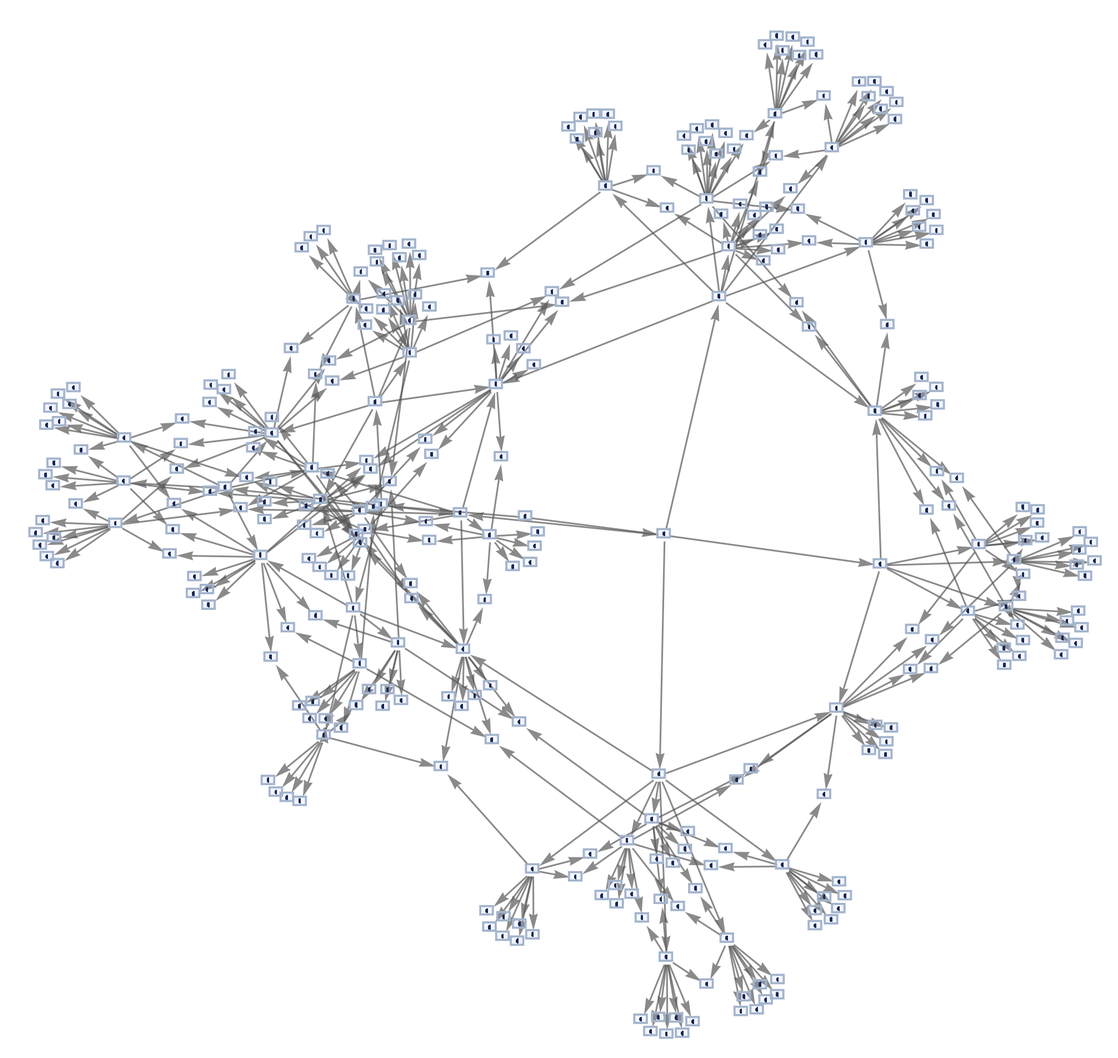
Так как это связано со временем? В нем говорится, что в основном утверждении модели есть не только один путь времени, есть много путей и много «историй». Но модель — и используемое правило — определяет их все. И мы увидели намек на кое-что еще: даже если мы можем подумать, что следуем «независимым» путем истории, он может фактически слиться с другим путем.

Чтобы объяснить, как все это работает, потребуются дополнительные исследования и дискуссии. Но пока позвольте мне сказать, что выясняется, что время — это причинно-следственные связи между событиями, и что на самом деле, даже когда исторические пути различаются, эти причинно-следственные связи могут оказаться одинаковыми. И по сути, для наблюдателя, встроенного в систему, остается только один поток времени.

Граф причинно-следственных связей

В итоге все выглядит чудесно элегантно. Но чтобы добраться до точки, где мы сможем понять всю большую картину, нам нужно подробнее разобрать некоторые аспекты. (Неудивительно, что фундаментальная теория физики — неизбежно построенная на очень абстрактных идеях — несколько сложна для объяснения, но иначе и быть не могло.)

Чтобы не усложнять задачу, я не буду говорить напрямую о правилах, действующих с гиперграфами. Вместо этого я собираюсь поговорить о правилах, которые работают со строками символов.

Скажем, у нас есть правило:
{A → BBB, BB → A}

Это правило гласит, что везде, где мы видим A, мы можем заменить его на BBB, и везде, где мы видим BB, мы можем заменить его на A. Итак, теперь мы можем сгенерировать то, что мы называем ветвящейся системой для этого правила, и нарисовать «граф ветвлений», который отображает все, что может случиться:


На первом шаге единственная возможность — использовать A → BBB для замены A на BBB. Но далее есть две возможности: заменить либо первый BB, либо второй BB — и эти варианты дают разные результаты. Однако на следующем этапе все, что можно сделать — это заменить букву A — в обоих случаях получая BBBB.

Другими словами, хотя в некотором смысле у нас было два исторических пути, которые расходились в системе ветвлений, потребовался всего один шаг, чтобы они снова слились. И если вы проследите рисунок выше, то обнаружите, что это всегда происходит с этим правилом: каждая создаваемая пара ветвей всегда сливается, в данном случае после еще одного шага.

Такой баланс между ветвлением и слиянием — явление, которое я называю причинно-следственной инвариантностью. И хотя в данном случае это может показаться мелочью, на самом деле оказывается, что это свойство наших моделей объясняет, почему работает теория относительности, почему в квантовой механике существует объективная реальность и множество других основных вопросов фундаментальной физики.

Давайте объясним, почему я называю это свойство причинно-следственной инвариантностью. На картинке выше показано, какое «состояние» (то есть какая строка) приводит к какому другому. Но рискуя усложнить картину (и обратите внимание, что это невероятно просто по сравнению со случаем полного гиперграфа), мы можем аннотировать многопутевой граф, включив в него события обновления, которые приводят к каждому переходу между состояниями:


Теперь мы можем задаться вопросом: каковы причинно-следственные связи между этими событиями? Другими словами, какое событие должно произойти, прежде чем может произойти какое-то другое событие? Или, другими словами, какие события должны были произойти, чтобы создать входные данные, необходимые для какого-то другого события?

Давайте пойдем еще дальше и аннотируем граф выше, показав все причинно-следственные зависимости между событиями:


Оранжевые линии показывают, какое событие должно произойти перед каким другим событием — или каковы все причинно-следственные связи в системе ветвлений. И да, это выглядит сложно. Но обратите внимание, что эта картина показывает всю систему ветвлений со всеми возможными историческими путями, а также всю сеть причинно-следственных связей внутри этих путей и между ними.

Но самое важное в причинной инвариантности то, что она подразумевает, что на самом деле граф причинно-следственных связей один и тот же, независимо от того, по какому историческому пути вы идете. И именно поэтому я первоначально назвал это свойство причинно-следственной инвариантностью — потому что в нем говорится, что с таким правилом, причинно-следственные свойства инвариантны по отношению к различным вариантам последовательности, в которой выполняется обновление.

И если еще раз взглянуть на рисунок выше (и пройти еще несколько шагов), можно обнаружить, что для каждого историческом пути причинно-следственный граф, отображающий причинно-следственные связи между событиями, всегда будет иметь вид:

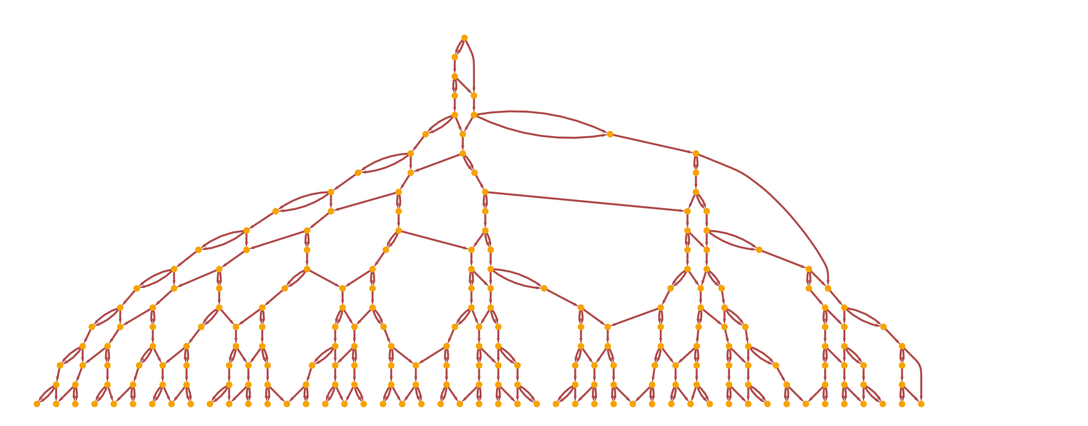
или, мы можем нарисовать его по-другому:

Важность причинно-следственной инвариантности

Чтобы лучше понять причинной-следственную инвариантность, полезно рассмотреть еще более простой пример: случай правила BA → AB. Это правило гласит, что каждый раз, когда в строке стоит буква B, за которой следует A, поменяйте местами эти символы. Другими словами, это правило пытается отсортировать строку в алфавитном порядке, по два символа за раз.

Допустим, мы начнем с BBBAAA. А вот граф ветвлений, показывающий все, что может произойти в соответствии с этим правилом:


Существует множество различных путей, по которым можно идти, в зависимости от того, к какому BA в строке применяется правило на каждом шаге. Но важно то, что мы видим, что в конце концов все пути сливаются, и мы получаем единственный конечный результат: отсортированную строку AAABBB. И тот факт, что мы получаем этот единственный конечный результат, является следствием причинно-следственной инвариантности правила. В таком случае, когда есть конечный результат (а не просто постоянное развитие), причинно-следственная инвариантность гласит: не имеет значения, в каком порядке вы выполняете все обновления, результат, который вы получите, всегда будет одним и тем же.

Я ввел причинно-следственную инвариантность в контексте попытки найти модель фундаментальной физики — и понял, что она будет иметь решающее значение как для теории относительности, так и для квантовой механики. Но на самом деле то, что равносильно причинно-следственной инвариантности, было замечено и раньше в различных формах математики, математической логики и информатики. (Его наиболее распространенное название — «ассоциативность», хотя есть некоторые технические различия между этим и тем, что я называю причинно-следственной инвариантностью.)

Подумайте о раскрытии алгебраического выражения, например (x + (1 + x)^2)(x + 2)^2. Неважно, в каком порядке вы будете выполнять шаги, вы всегда получите один и тот же результат (в данном случае 4 + 16x + 17x^2 + 7x^3 + x^4). И эта независимость порядков по сути является причинно-следственной инвариантностью.

Еще один пример. Представьте, что у вас есть рекурсивное определение, скажем: f[n_]:=f[n-1]+f[n-2] (c f[0]=f[1]=1). Теперь попробуем вычислить f[10]. Сначала вы получите f[9]+f[8]. Что вы вычислите потом: f[9] или f[8]? Это не имеет никакого значения. Результат всегда будет равен 55. И это еще один пример причинно-следственной инвариантности.

Те, кто имеет опыт работы с параллельными или асинхронными алгоритмами, знают, что очень важно, имеет ли этот алгоритм причинно-следственную инвариантность. Потому что это означает, что можно делать что-то в любом порядке — скажем, в глубину, в ширину или что-то еще — и всегда получишь один и тот же ответ. То же самое происходит в нашем небольшом алгоритме сортировки выше.

Хорошо, но теперь вернемся к причинно-следственным связям. Вот система ветвлений для процесса сортировки с аннотациями всех причинно-следственных связей для всех путей:


Это беспорядок. Но поскольку существует причинно-следственная инвариантность, мы знаем кое-что очень важное: это просто множество копий одного и того же причинно-следственного графа — простой сетки:


Между прочим — как видно из рисунка — перекрестные связи между этими копиями нетривиальны, и позже мы увидим, что они связаны с глубокими отношениями между теорией относительности и квантовой механикой, которые, вероятно, проявляются в физике черных дыр. Но мы вернемся к этому позже…

Предполагается, что каждый другой способ применения правила сортировки дает один и тот же причинно-следственный граф. Итак, вот один пример того, как мы можем применить правило, начиная с конкретной начальной строки:


А теперь покажем граф причинно-следственных связей. И мы видим, что это просто сетка:


Вот еще три возможных последовательности обновлений:


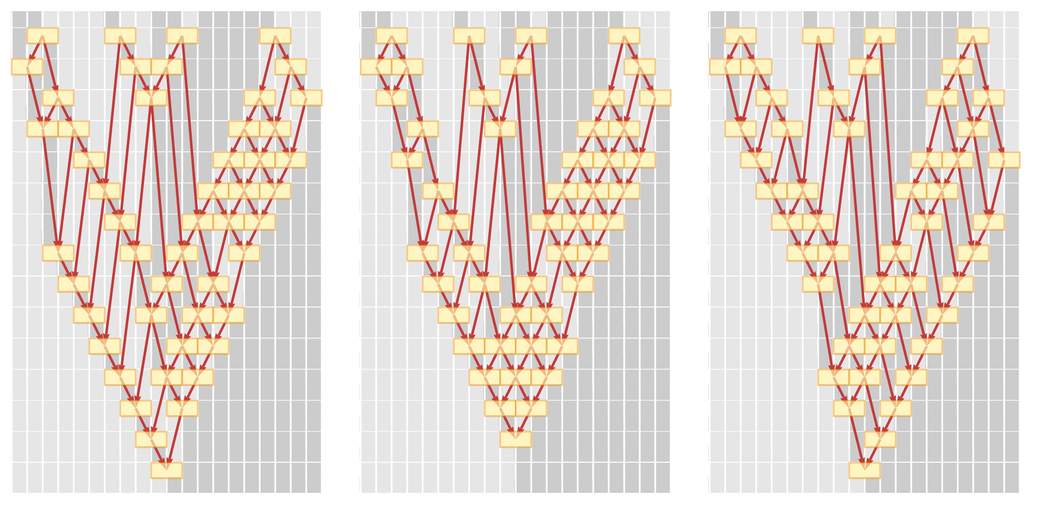
Теперь мы видим причинно-следственную инвариантность в действии: хотя разные обновления происходят в разное время, граф причинно-следственных связей между событиями обновления всегда один и тот же. И, увидев это — в контексте очень простого примера, — мы готовы поговорить о специальной теории относительности.

Вывод специальной теории относительности

Как правило, занимаясь наукой, вы представляете, как проводите эксперимент над системой, но вы — как «наблюдатель» — находитесь вне системы. Конечно, если вы думаете о моделировании всей вселенной и всего в ней существующего, это не совсем разумный способ думать о системе. Потому что наблюдатель неизбежно является частью Вселенной, и поэтому его нужно моделировать, как и все остальное.

В наших моделях это означает, что «разум наблюдателя», как и все остальное во Вселенной, должен обновляться через серию событий. Для наблюдателя нет абсолютного способа узнать, что происходит во Вселенной. Все, что они когда-либо испытывали, — это серия событий обновления, на которые могут повлиять события обновления, происходящие где-то в другом месте вселенной. Или, говоря иначе, все, что наблюдатель может когда-либо наблюдать, — это сеть причинно-следственных связей между событиями — или причинно-следственный граф, о котором мы говорили.

В качестве игрушечной модели давайте посмотрим на наше правило BA → AB для строк. Можно представить себе, что строка лежит в пространстве. Но единственное, что видит наш наблюдатель — это причинно-следственный граф, который представляет причинно-следственные связи между событиями. А для системы BA → AB это можно сделать следующим образом:


Но теперь давайте подумаем о том, как наблюдатели могут «ощутить» этот причинно-следственный граф. Наблюдатель сам по себе обновляется посредством некоторой последовательности событий. Но даже несмотря на то, что это «действительно то, что происходит», чтобы понять это, мы можем представить, что наши наблюдатели создают внутренние «ментальные» модели того, что они видят. И для таких наблюдателей, как мы, довольно естественно просто сказать: «Один набор событий происходит по всей вселенной, затем другой и так далее». И мы можем перевести это на человеческий, сказав, что мы представляем серию «моментов» во времени, когда вещи происходят «одновременно» по всей вселенной — по крайней мере, с некоторыми соглашениями для определения того, что мы подразумеваем под одновременным. (И да, эти идеи сходны с идеями Эйнштейна в то время, когда он создал специальную теорию относительности.)

Вот возможный способ сделать это:


Это можно описать как «слоение» причинно-следственного графа. Мы делим причинно-следственный граф на срезы. И каждый срез наши наблюдатели могут рассматривать как «последовательный момент времени».

Важно отметить, что есть некоторые ограничения на выбор слоения. Причинно-следственный граф определяет, какое событие должно произойти до чего. И если у наших наблюдателей будет шанс осмыслить мир, лучше всего, если их представление о ходе времени согласуется с тем, что говорит причинно-следственный граф. Так, например, это слоение не будет работать — потому что оно говорит, что время, которое мы назначаем событиям, не согласуется с порядком, в котором они должны произойти:


Какой фактический порядок обновления событий подразумевает приведенное выше слоение? По сути, как можно больше событий должно происходить одновременно (то есть в одном и том же срезе слоения), как на этой картинке:


Теперь давайте свяжем это с физикой. Слоение, которое у нас было выше, относится к наблюдателям, которые каким-то образом «неподвижны по отношению ко Вселенной» («космологическая система покоя»). Можно представить себе, что с течением времени события, которые переживает конкретный наблюдатель, помещаются в столбец, идущий вертикально вниз по графу:


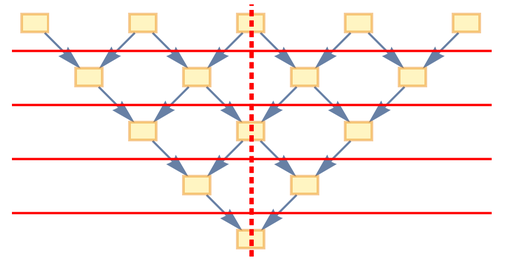
Но теперь давайте подумаем о наблюдателе, который равномерно движется в пространстве. У них будет другая последовательность событий, например такая:


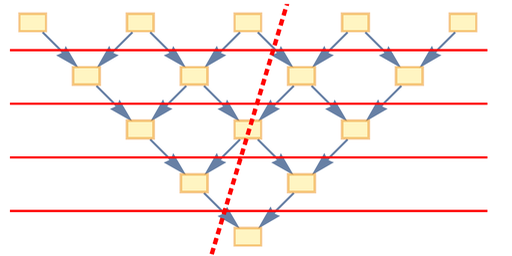
А это значит, что слоение, которое они построят естественным образом, будет другим. «Со стороны» мы можем нарисовать это на причинно-следственном графе следующим образом:


Но для наблюдателя каждый срез представляет собой последовательный момент времени. И у них нет никакого способа узнать, как был нарисован причинно-следственный граф. Таким образом, они построят свою собственную версию с горизонтальными срезами:


Теперь мы видим чисто геометрический факт: чтобы произвести эту перестановку, сохраняя при этом базовую структуру (а здесь и углы) причинно-следственного графа, каждый момент времени нужно отбирать меньше событий в причинном графе c коэффициэнтом sqrt(1 - β^2), где β равно угол, который представляет скорость наблюдателя.

Если вы что-то понимаете в специальной теории относительности, то вы узнаете многое из этого. То, что мы называем слоениями, соответствует «системам отсчета» теории относительности. И наши слоения, представляющие движение, являются стандартными инерциальными системами отсчета специальной теории относительности.

Здесь есть особенно интересный момент: мы можем интерпретировать все это обсуждение слоений и систем отсчета с точки зрения реальных правил эволюции нашей базовой системы. Итак, вот эволюция нашей системы сортировки строк в инерциальной системе отсчета, соответствующей наблюдателю, движущемуся с определенной скоростью:


Из-за причинно-следственной инвариантности не имеет значения, что мы находимся в другой системе отсчета — причинно-следственный граф для системы (и способ, которым он в конечном итоге сортирует строку) точно такой же.

Основная идея специальной теории относительности состоит в том, что законы физики работают одинаково во всех инерциальных системах отсчета. Но почему это должно быть правдой? Что ж, в наших системах есть ответ: это следствие причинно-следственной инвариантности основных правил. Другими словами, из свойства причинно-следственной инвариантности мы можем вывести относительность.

Обычно в физике относительность вводится путем установления математической структуры пространства-времени. Но в наших моделях мы не делаем ничего подобного, и на самом деле пространство и время вовсе не одно и то же. Теперь мы видим, что из-за причинно-следственной инвариантности в наших моделях появляется относительность со всеми связями между пространством и временем, которые она подразумевает.

Опубликовано на сайте: 2020-11-08